相邻节点迭代器

图论中最常见的操作就是遍历邻边，通过一个顶点遍历相关的邻边。邻接矩阵的遍历邻边的时间复杂度为 O(V)，邻接表可以直接找到，效率更高。

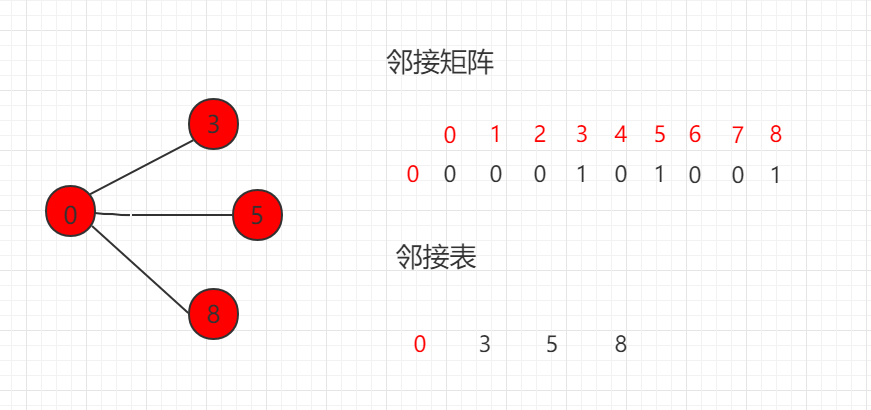
邻接矩阵迭代:

...
public Iterable<Integer> adj(int v) {
    assert v >= 0 && v < n;
    Vector<Integer> adjV = new Vector<Integer>();
    for(int i = 0 ; i < n ; i ++ )
        if( g[v][i] )
            adjV.add(i);
    return adjV;
}
...

邻接表迭代：

...
// 返回图中一个顶点的所有邻边
// 由于java使用引用机制，返回一个Vector不会带来额外开销,
public Iterable<Integer> adj(int v) {
    assert v >= 0 && v < n;
    return g[v];
}
...

对于这两种图的表达方式我们可以抽象出一个接口，生成这一套算法的框架，而不用去考虑底层是邻接表还是邻接矩阵。

本小节写了一个测试用例 GraphReadTest，通过调用抽象接口实现图的展示，可以在 read 包查看。

/**
 * 图的抽象接口
 */
public interface Graph {
    public int V();
    public int E();
    public void addEdge( int v , int w );
    boolean hasEdge( int v , int w );
    void show();
    public Iterable<Integer> adj(int v);
}

Java 实例代码

源码包下载：Download

（1）邻接矩阵迭代

src/haodaima/graph/DenseGraphIterater.java 文件代码：

package haodaima.graph;

import java.util.Vector;

/**
 * 邻接矩阵迭代
 */
public class DenseGraphIterater {
    // 节点数
    private int n;
    // 边数
    private int m;
    // 是否为有向图
    private boolean directed;
    // 图的具体数据
    private boolean[][] g;

    // 构造函数
    public DenseGraphIterater( int n , boolean directed ){
        assert n >= 0;
        this.n = n;
        this.m = 0;
        this.directed = directed;
        // g初始化为n*n的布尔矩阵, 每一个g[i][j]均为false, 表示没有任和边
        // false为boolean型变量的默认值
        g = new boolean[n][n];
    }
    // 返回节点个数
    public int V(){ return n;}
    // 返回边的个数
    public int E(){ return m;}

    // 向图中添加一个边
    public void addEdge( int v , int w ){
        assert v >= 0 && v < n ;
        assert w >= 0 && w < n ;
        if( hasEdge( v , w ) )
            return;
        g[v][w] = true;
        if( !directed )
            g[w][v] = true;
        m ++;
    }

    // 验证图中是否有从v到w的边
    boolean hasEdge( int v , int w ){
        assert v >= 0 && v < n ;
        assert w >= 0 && w < n ;
        return g[v][w];
    }
    // 返回图中一个顶点的所有邻边
    // 由于java使用引用机制，返回一个Vector不会带来额外开销,
    public Iterable<Integer> adj(int v) {
        assert v >= 0 && v < n;
        Vector<Integer> adjV = new Vector<Integer>();
        for(int i = 0 ; i < n ; i ++ )
            if( g[v][i] )
                adjV.add(i);
        return adjV;
    }
}

（2）邻接表迭代

src/haodaima/graph/SparseGraphIterater.java 文件代码：

package haodaima.graph;

import java.util.Vector;

/**
 * 邻接表迭代
 */
public class SparseGraphIterater {

    private int n;  // 节点数
    private int m;  // 边数
    private boolean directed;    // 是否为有向图
    private Vector<Integer>[] g; // 图的具体数据

    // 构造函数
    public SparseGraphIterater( int n , boolean directed ){
        assert n >= 0;
        this.n = n;
        this.m = 0;    // 初始化没有任何边
        this.directed = directed;
        // g初始化为n个空的vector, 表示每一个g[i]都为空, 即没有任和边
        g = (Vector<Integer>[])new Vector[n];
        for(int i = 0 ; i < n ; i ++)
            g[i] = new Vector<Integer>();
    }
    public int V(){ return n;} // 返回节点个数
    public int E(){ return m;} // 返回边的个数

    // 向图中添加一个边
    public void addEdge( int v, int w ){

        assert v >= 0 && v < n ;
        assert w >= 0 && w < n ;

        g[v].add(w);
        if( v != w && !directed )
            g[w].add(v);

        m ++;
    }

    // 验证图中是否有从v到w的边
    boolean hasEdge( int v , int w ){

        assert v >= 0 && v < n ;
        assert w >= 0 && w < n ;

        for( int i = 0 ; i < g[v].size() ; i ++ )
            if( g[v].elementAt(i) == w )
                return true;
        return false;
    }

    // 返回图中一个顶点的所有邻边
    // 由于java使用引用机制，返回一个Vector不会带来额外开销,
    public Iterable<Integer> adj(int v) {
        assert v >= 0 && v < n;
        return g[v];
    }
}