二分搜索树节点删除
本小节介绍二分搜索树节点的删除之前,先介绍如何查找最小值和最大值,以及删除最小值和最大值。
以最小值为例(最大值同理):
查找最小 key 值代码逻辑,往左子节点递归查找下去:
...
// 返回以node为根的二分搜索树的最小键值所在的节点
private Node minimum(Node node){
if( node.left == null )
return node;
return minimum(node.left);
}
...
// 返回以node为根的二分搜索树的最小键值所在的节点
private Node minimum(Node node){
if( node.left == null )
return node;
return minimum(node.left);
}
...
删除二分搜索树的最小 key 值,如果该节点没有右子树,那么直接删除,如果存在右子树,如图所示:
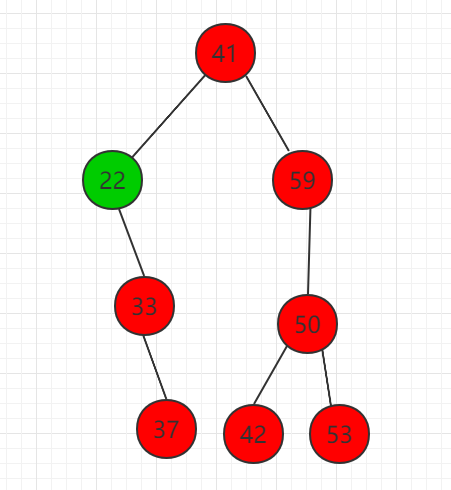
删除节点 22,存在右孩子,只需要将右子树 33 节点代替节点 22。
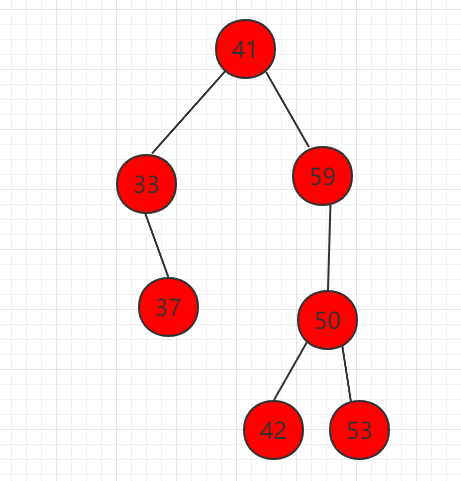
这个删除最小值用代码表示:
...
// 删除掉以node为根的二分搜索树中的最小节点
// 返回删除节点后新的二分搜索树的根
private Node removeMin(Node node){
if( node.left == null ){
Node rightNode = node.right;
node.right = null;
count --;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
...
// 删除掉以node为根的二分搜索树中的最小节点
// 返回删除节点后新的二分搜索树的根
private Node removeMin(Node node){
if( node.left == null ){
Node rightNode = node.right;
node.right = null;
count --;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
...
现在讨论二分搜索树节点删除分以下三种情况:
1、删除只有左孩子的节点,如下图节点 58。

删除掉元素 58,让左子树直接代替 58 的位置,整个二分搜索树的性质不变。
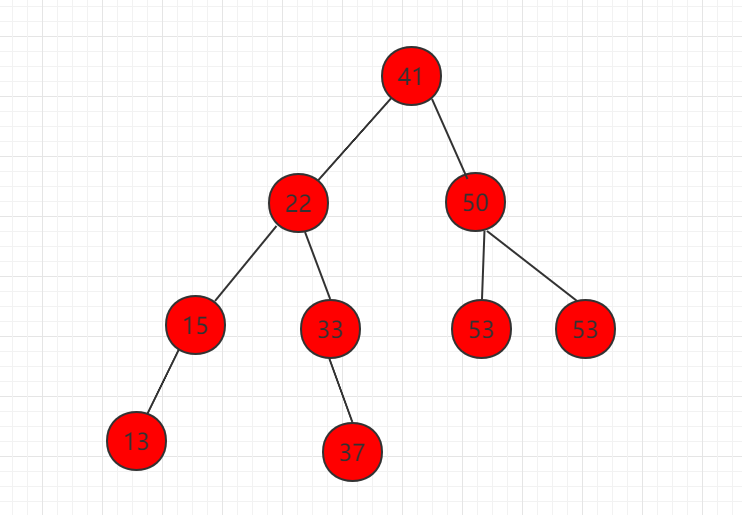
2、删除只有右孩子的节点,如下图节点 58。
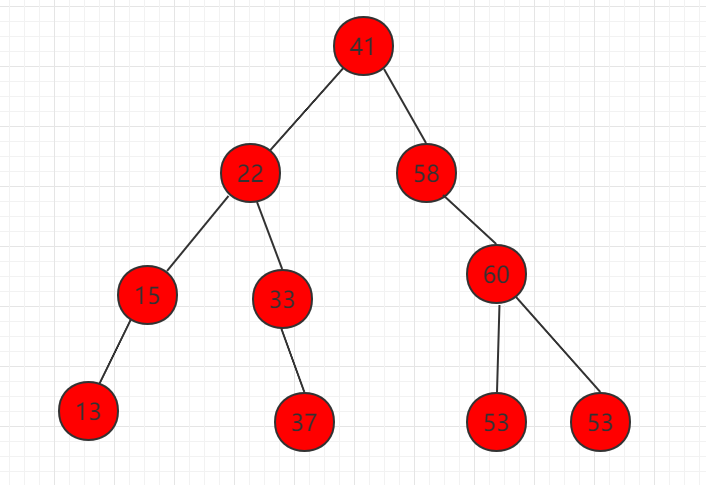
删除掉元素 58,让右子树直接代替 58 的位置,整个二分搜索树的性质不变。
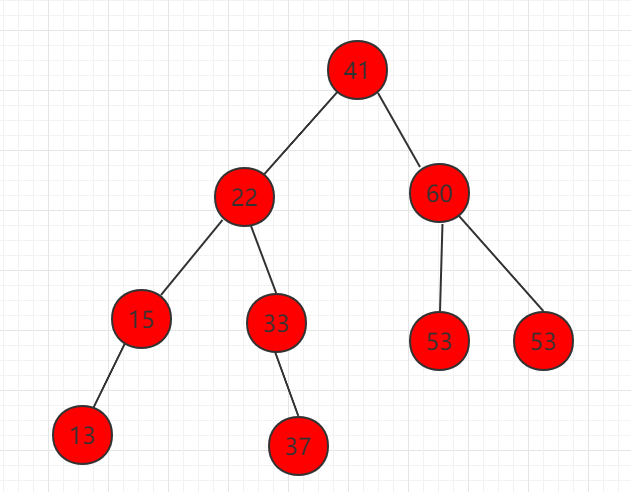
3、删除左右都有孩子的节点,如下图节点 58。

(1)找到右子树中的最小值,为节点 59
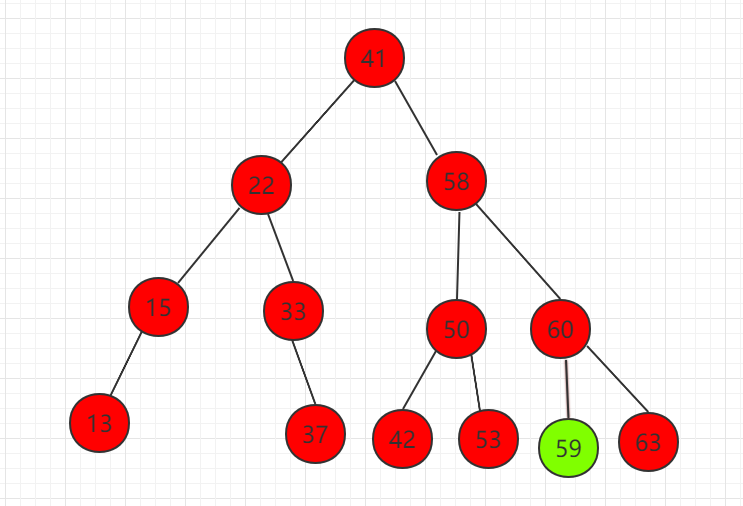
(2)节点 59 代替待删除节点 58
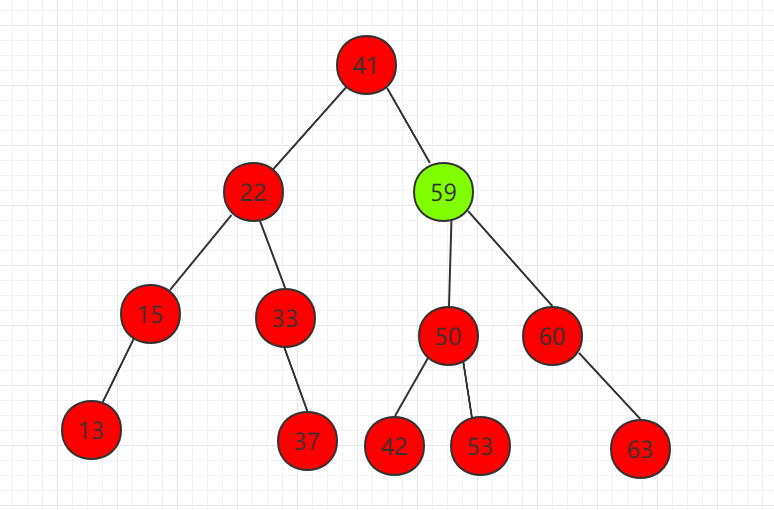
综合以上规律,删除以 node 为根的二分搜索树中键值为 key 的节点,核心代码示例:
源码包下载:Download
src/haodaima/binary/BSTRemove.java 文件代码:
package haodaima.binary;
import java.util.LinkedList;
/**
* 二分搜索树节点删除
*/
public class BSTRemove<Key extends Comparable<Key>, Value> {
// 树中的节点为私有的类, 外界不需要了解二分搜索树节点的具体实现
private class Node {
private Key key;
private Value value;
private Node left, right;
public Node(Key key, Value value) {
this.key = key;
this.value = value;
left = right = null;
}
public Node(Node node){
this.key = node.key;
this.value = node.value;
this.left = node.left;
this.right = node.right;
}
}
private Node root; // 根节点
private int count; // 树种的节点个数
// 构造函数, 默认构造一棵空二分搜索树
public BSTRemove() {
root = null;
count = 0;
}
// 返回二分搜索树的节点个数
public int size() {
return count;
}
// 返回二分搜索树是否为空
public boolean isEmpty() {
return count == 0;
}
// 向二分搜索树中插入一个新的(key, value)数据对
public void insert(Key key, Value value){
root = insert(root, key, value);
}
// 查看二分搜索树中是否存在键key
public boolean contain(Key key){
return contain(root, key);
}
// 在二分搜索树中搜索键key所对应的值。如果这个值不存在, 则返回null
public Value search(Key key){
return search( root , key );
}
// 二分搜索树的前序遍历
public void preOrder(){
preOrder(root);
}
// 二分搜索树的中序遍历
public void inOrder(){
inOrder(root);
}
// 二分搜索树的后序遍历
public void postOrder(){
postOrder(root);
}
// 二分搜索树的层序遍历
public void levelOrder(){
// 我们使用LinkedList来作为我们的队列
LinkedList<Node> q = new LinkedList<Node>();
q.add(root);
while( !q.isEmpty() ){
Node node = q.remove();
System.out.println(node.key);
if( node.left != null )
q.add( node.left );
if( node.right != null )
q.add( node.right );
}
}
// 寻找二分搜索树的最小的键值
public Key minimum(){
assert count != 0;
Node minNode = minimum( root );
return minNode.key;
}
// 寻找二分搜索树的最大的键值
public Key maximum(){
assert count != 0;
Node maxNode = maximum(root);
return maxNode.key;
}
// 从二分搜索树中删除最小值所在节点
public void removeMin(){
if( root != null )
root = removeMin( root );
}
// 从二分搜索树中删除最大值所在节点
public void removeMax(){
if( root != null )
root = removeMax( root );
}
// 从二分搜索树中删除键值为key的节点
public void remove(Key key){
root = remove(root, key);
}
//********************
//* 二分搜索树的辅助函数
//********************
// 向以node为根的二分搜索树中, 插入节点(key, value), 使用递归算法
// 返回插入新节点后的二分搜索树的根
private Node insert(Node node, Key key, Value value){
if( node == null ){
count ++;
return new Node(key, value);
}
if( key.compareTo(node.key) == 0 )
node.value = value;
else if( key.compareTo(node.key) < 0 )
node.left = insert( node.left , key, value);
else // key > node->key
node.right = insert( node.right, key, value);
return node;
}
// 查看以node为根的二分搜索树中是否包含键值为key的节点, 使用递归算法
private boolean contain(Node node, Key key){
if( node == null )
return false;
if( key.compareTo(node.key) == 0 )
return true;
else if( key.compareTo(node.key) < 0 )
return contain( node.left , key );
else // key > node->key
return contain( node.right , key );
}
// 在以node为根的二分搜索树中查找key所对应的value, 递归算法
// 若value不存在, 则返回NULL
private Value search(Node node, Key key){
if( node == null )
return null;
if( key.compareTo(node.key) == 0 )
return node.value;
else if( key.compareTo(node.key) < 0 )
return search( node.left , key );
else // key > node->key
return search( node.right, key );
}
// 对以node为根的二叉搜索树进行前序遍历, 递归算法
private void preOrder(Node node){
if( node != null ){
System.out.println(node.key);
preOrder(node.left);
preOrder(node.right);
}
}
// 对以node为根的二叉搜索树进行中序遍历, 递归算法
private void inOrder(Node node){
if( node != null ){
inOrder(node.left);
System.out.println(node.key);
inOrder(node.right);
}
}
// 对以node为根的二叉搜索树进行后序遍历, 递归算法
private void postOrder(Node node){
if( node != null ){
postOrder(node.left);
postOrder(node.right);
System.out.println(node.key);
}
}
// 返回以node为根的二分搜索树的最小键值所在的节点
private Node minimum(Node node){
if( node.left == null )
return node;
return minimum(node.left);
}
// 返回以node为根的二分搜索树的最大键值所在的节点
private Node maximum(Node node){
if( node.right == null )
return node;
return maximum(node.right);
}
// 删除掉以node为根的二分搜索树中的最小节点
// 返回删除节点后新的二分搜索树的根
private Node removeMin(Node node){
if( node.left == null ){
Node rightNode = node.right;
node.right = null;
count --;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
// 删除掉以node为根的二分搜索树中的最大节点
// 返回删除节点后新的二分搜索树的根
private Node removeMax(Node node){
if( node.right == null ){
Node leftNode = node.left;
node.left = null;
count --;
return leftNode;
}
node.right = removeMax(node.right);
return node;
}
// 删除掉以node为根的二分搜索树中键值为key的节点, 递归算法
// 返回删除节点后新的二分搜索树的根
Node remove(Node node, Key key){
if( node == null )
return null;
if( key.compareTo(node.key) < 0 ){
node.left = remove( node.left , key );
return node;
}
else if( key.compareTo(node.key) > 0 ){
node.right = remove( node.right, key );
return node;
}
else{ // key == node->key
// 待删除节点左子树为空的情况
if( node.left == null ){
Node rightNode = node.right;
node.right = null;
count --;
return rightNode;
}
// 待删除节点右子树为空的情况
if( node.right == null ){
Node leftNode = node.left;
node.left = null;
count--;
return leftNode;
}
// 待删除节点左右子树均不为空的情况
// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor = new Node(minimum(node.right));
count ++;
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
count --;
return successor;
}
}
}
import java.util.LinkedList;
/**
* 二分搜索树节点删除
*/
public class BSTRemove<Key extends Comparable<Key>, Value> {
// 树中的节点为私有的类, 外界不需要了解二分搜索树节点的具体实现
private class Node {
private Key key;
private Value value;
private Node left, right;
public Node(Key key, Value value) {
this.key = key;
this.value = value;
left = right = null;
}
public Node(Node node){
this.key = node.key;
this.value = node.value;
this.left = node.left;
this.right = node.right;
}
}
private Node root; // 根节点
private int count; // 树种的节点个数
// 构造函数, 默认构造一棵空二分搜索树
public BSTRemove() {
root = null;
count = 0;
}
// 返回二分搜索树的节点个数
public int size() {
return count;
}
// 返回二分搜索树是否为空
public boolean isEmpty() {
return count == 0;
}
// 向二分搜索树中插入一个新的(key, value)数据对
public void insert(Key key, Value value){
root = insert(root, key, value);
}
// 查看二分搜索树中是否存在键key
public boolean contain(Key key){
return contain(root, key);
}
// 在二分搜索树中搜索键key所对应的值。如果这个值不存在, 则返回null
public Value search(Key key){
return search( root , key );
}
// 二分搜索树的前序遍历
public void preOrder(){
preOrder(root);
}
// 二分搜索树的中序遍历
public void inOrder(){
inOrder(root);
}
// 二分搜索树的后序遍历
public void postOrder(){
postOrder(root);
}
// 二分搜索树的层序遍历
public void levelOrder(){
// 我们使用LinkedList来作为我们的队列
LinkedList<Node> q = new LinkedList<Node>();
q.add(root);
while( !q.isEmpty() ){
Node node = q.remove();
System.out.println(node.key);
if( node.left != null )
q.add( node.left );
if( node.right != null )
q.add( node.right );
}
}
// 寻找二分搜索树的最小的键值
public Key minimum(){
assert count != 0;
Node minNode = minimum( root );
return minNode.key;
}
// 寻找二分搜索树的最大的键值
public Key maximum(){
assert count != 0;
Node maxNode = maximum(root);
return maxNode.key;
}
// 从二分搜索树中删除最小值所在节点
public void removeMin(){
if( root != null )
root = removeMin( root );
}
// 从二分搜索树中删除最大值所在节点
public void removeMax(){
if( root != null )
root = removeMax( root );
}
// 从二分搜索树中删除键值为key的节点
public void remove(Key key){
root = remove(root, key);
}
//********************
//* 二分搜索树的辅助函数
//********************
// 向以node为根的二分搜索树中, 插入节点(key, value), 使用递归算法
// 返回插入新节点后的二分搜索树的根
private Node insert(Node node, Key key, Value value){
if( node == null ){
count ++;
return new Node(key, value);
}
if( key.compareTo(node.key) == 0 )
node.value = value;
else if( key.compareTo(node.key) < 0 )
node.left = insert( node.left , key, value);
else // key > node->key
node.right = insert( node.right, key, value);
return node;
}
// 查看以node为根的二分搜索树中是否包含键值为key的节点, 使用递归算法
private boolean contain(Node node, Key key){
if( node == null )
return false;
if( key.compareTo(node.key) == 0 )
return true;
else if( key.compareTo(node.key) < 0 )
return contain( node.left , key );
else // key > node->key
return contain( node.right , key );
}
// 在以node为根的二分搜索树中查找key所对应的value, 递归算法
// 若value不存在, 则返回NULL
private Value search(Node node, Key key){
if( node == null )
return null;
if( key.compareTo(node.key) == 0 )
return node.value;
else if( key.compareTo(node.key) < 0 )
return search( node.left , key );
else // key > node->key
return search( node.right, key );
}
// 对以node为根的二叉搜索树进行前序遍历, 递归算法
private void preOrder(Node node){
if( node != null ){
System.out.println(node.key);
preOrder(node.left);
preOrder(node.right);
}
}
// 对以node为根的二叉搜索树进行中序遍历, 递归算法
private void inOrder(Node node){
if( node != null ){
inOrder(node.left);
System.out.println(node.key);
inOrder(node.right);
}
}
// 对以node为根的二叉搜索树进行后序遍历, 递归算法
private void postOrder(Node node){
if( node != null ){
postOrder(node.left);
postOrder(node.right);
System.out.println(node.key);
}
}
// 返回以node为根的二分搜索树的最小键值所在的节点
private Node minimum(Node node){
if( node.left == null )
return node;
return minimum(node.left);
}
// 返回以node为根的二分搜索树的最大键值所在的节点
private Node maximum(Node node){
if( node.right == null )
return node;
return maximum(node.right);
}
// 删除掉以node为根的二分搜索树中的最小节点
// 返回删除节点后新的二分搜索树的根
private Node removeMin(Node node){
if( node.left == null ){
Node rightNode = node.right;
node.right = null;
count --;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
// 删除掉以node为根的二分搜索树中的最大节点
// 返回删除节点后新的二分搜索树的根
private Node removeMax(Node node){
if( node.right == null ){
Node leftNode = node.left;
node.left = null;
count --;
return leftNode;
}
node.right = removeMax(node.right);
return node;
}
// 删除掉以node为根的二分搜索树中键值为key的节点, 递归算法
// 返回删除节点后新的二分搜索树的根
Node remove(Node node, Key key){
if( node == null )
return null;
if( key.compareTo(node.key) < 0 ){
node.left = remove( node.left , key );
return node;
}
else if( key.compareTo(node.key) > 0 ){
node.right = remove( node.right, key );
return node;
}
else{ // key == node->key
// 待删除节点左子树为空的情况
if( node.left == null ){
Node rightNode = node.right;
node.right = null;
count --;
return rightNode;
}
// 待删除节点右子树为空的情况
if( node.right == null ){
Node leftNode = node.left;
node.left = null;
count--;
return leftNode;
}
// 待删除节点左右子树均不为空的情况
// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor = new Node(minimum(node.right));
count ++;
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
count --;
return successor;
}
}
}